|
|
Boston University CS 580
Assignment 3
Masha Shugrina
Problem Summary:
To implement radiosity algorithm for modeling diffuse reflections within a closed environment
represented modeled using quadrilateral geometric primitives.
Algorithm:
The algorithm can be summarized using the following components:
1. Subdivide the Scene
The scene is input as a text file composed of octahedrons and quadrilaterals,
which are subdivided into patches of roughly equal dimensions based on the constant
maximum patch size. The patches are stored in a quad-tree representation as
follows:

The original imput patches of the quadrilateral geometric primitives are
each subdivided into 4 sub-patches. The process continues recursively until the
pre-specified patch width is reached. Then, during the initalization process of the scene,
the leaves are connected linked into a singly linked list. These leaf patches
are referred to by indices i and j in the following duscussion.
2. Iterative Radiosity Solution
Radiosity is based on computing the light energy reflected from patch to
patch within the scene using a large linear equation system. Because computing
the exact solution is very computationally expensive, iterative methods are preferable.
This project implements the Progressive Radiosity iterative algorithm:
&forall patches i Bi = Ei, &Delta Bi = Ei
while not converged
pick i s.t. &Delta Bi*Ai is maximal
for every other patch j
&Delta rad = &Delta Bi*&rhojFji
&Delta Bj += &Delta rad
Bj += &Delta rad
&Delta Bi = 0
display intermediate image result
Here, &rho is the reflectance of the patch.
This method eliminates the necessity of evaluating every possible Form Factor,
and hence attains greater efficiency. Additionally, it allows the intermediate
result to be displayed.
3. Form Factor Computation
Form Factor Fij
is defined as the light energy that reaches patch j from patch i divided by the total
light energy reflected from patch i, or mathematically:
Fij= 1/Ai&int Ai&int Aj[cos &phii cos &phij/&phi r2] dAjdAi
where Ai and Aj are the areas of patches i and j, dA's are the differential
areas, and &phi 's are angles formed between the line connecting the differential areas and their
respective normals.
Because the closed form of this integral is highly impractical, a number of numerical
approximation techniques have been devised. This project implementes the Monte Carlo algorithm,
that can be summarized as follows:

from the center of patch i shoot out N rays, uniformly distributed over the hemisphere
set up an array F[num_patches]
for each ray r
compute the intersection with the closest other patch j in the scene
F[num_patches] += cos &phii cos &phij/&phi r2
from each entry j in F obtain the following
Fij = F[j]*Aj/N
Fji = F[j]*Ai/N
Hence, at each step in the progressive radiosity algorithm, a whole row of Form Factors is
computed. The relationship FjiAj= FijAi is utilized
to avoid overcomputation. The ray-scene intersection is made more efficient for simple quadrilateral
models by the quad tree representation: first the intersection points are computed for each mother patch,
and then the intersected leaf within the patch subtree is identified via inside/outside plane tests (two
for each step down the tree).
4. Error Computation
For a scene with n patches the radiosity linear equation problem can be formulated in terms of the KB=E matrix
equation, where K is an n*n matrix with K[i][j] = -&rhoiFij and 1's across
across the diagonal, E is the n*1 vector of emission coefficients for each patch, and B is the n*1 vector
of unknown radiosity values for each patch in the scene. Given this information, the error, termed the residual,
is computed as follows:
R = KB-E,
where B is the estimated radiosity solution. The length of this vector can be used as the
convergence criterion for the Progressive Radiosity, and for the implementation of adaptive subdivision.
However, because the value of the residual that produces the desired image is to be determined empirically,
this implementation provides user with the maximum control of the resultant image. The algorithm automatically
runs for #iterations n = #patches/10, and the user is given the freedom to request another round of n
iterations. This feedback loop approach seems to me more trustworthy and artistically feasible than the
residual computation. After all, the scene may look better in a pre-convergence gloom.
5. Adaptive Subdivision
This is a possible extension of the system.
6. Rendering
During the subdivision process, the vertices of the newly-created sub-patches are not duplicated. Each vertex keeps track
of its 4 (or less) immediate neighboring patches. Before rendering, the color of each vertex is computed by averaging
the radiosities of the neighboring patches. Then, rendering is performed using OpenGL smooth polygon
shading. Back-face culling is enabled.
Results:
Cornell Box:
The following images were produced using a subdivision model of order of 2,000 patches.
These two images show the vertex to patch pointers used to interpolate the radiosity values
of the patches.


These are intermediate results for 50, 300 and 1000 iterations of the Progressive Radiosity Algorithm, respectively.
(Click to enlarge).



These are three views of the final result achieved with about 1200 iterations.



Cafe:
The first image was produced with 2700 patches, 1000 iterations and took approximately 15 minutes on
a 1.73 GHz processor. The second and third images were achieved with 680 patches and 400 iterations:
they deomonstrate the need of adaptive subdivision for scenes with small objects (notice the peculiar
"lack" if shadows due to interpolation over oversized patches).



Miscellaneous Room:
This was achieved via 800 iterations for a 700 patch model. The images show uninterpolated, interpolated,
wireframe and vertex-to-patch-connections views.



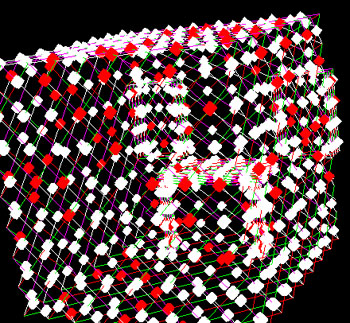
The results are rather convincing even without adaptive subdivision, however, the system as it is now
cannot produce nice sharp shados, especially from thing objects s.a. table legs. However, the system
has been designed to allow for this modification, and this extensions would be fairly simple to
implement.
Program:
The program is a simple console application built in VC++. It compiles and runs on Windows using the
OpenCV and OpenGL libraries. The expected input is a text file, the specifications for which as well
as other useful information can be found in the README file. The most important files in the bundle
are scene.cpp and geomTypes.cpp.
Download All Files
|














