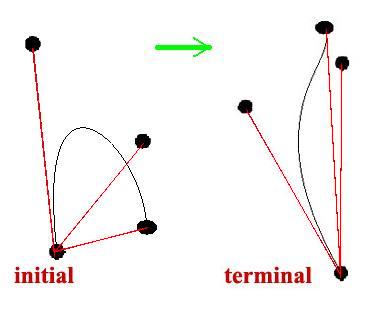
Boston University CS 580
Final Project
Masha Shugrina

Problem Summary:

To model the development of the above blossoms and to create continuous animation of their development using the dL-system method.

General Method:

The algorithm is based on the work of Prusinkiewicz et al [1], that extends the discretized approach for producing recursively branching structures (L-systems) to continuous domain in order to produce animation of plant development (dL-systmes). L-Systems model plant development by a set of rewriting rules that transform a particular plant element P (i.e. branch, etc.) to another element(s) (for instance, to the former branch and two new sub-branches): 
[P] &larr [R1P'1][R2P'2],
where R is some transformation matrix. dL-systems model the continuous transformation of a plant element P between these discretized steps, where P now has continuously varying parameter vector x: 
P(x):
    if(x < xmax)
        solve for &Delta x
        x &larr x + &Delta x
    else 
        produce P(x) &larr P(x)[R1P'1(x0)][R2P'2(x0)],
where x could represent a threshold length up to which the branch grows before splitting.
Because plants often develop sigmoidally (initially grow slowly, then accelerate, then level off near the maximum value), the growth function used for calculating most &Delta x's in this project was Velhurst's logistic function, as suggested by [1]: 
 dx/dt = r (1 - x / xmax) x,
where r is a constant parameter. Although a closed form solution for this differential equation exists, it is more convenient to use Euler's forward method for approximating the solution at discrete steps &Delta T.

Particulars & Results:

Click on the icons to watch clips.

1. Growing the Branch:
The branch is grown only once using L-systems and randomization for more realistic results. There are four branch elements: Internode, Dead Node, Alive Node, Apex. In this implementation, only the apex is rewritten: Apex &larr [R1 P1][R2P2], where each Pi can be any one of the four branch elements, as determined by preset probabilities of different splits.

2. Flowering Apex:
Growth of the flowering apex, A(x,n,a), depends on n, the number of flowers it contains (up to some perturbed maximum number),and a, the current "active length." Upon reaching a threshold a, the apex transforms discontinuously, producing another flower stem, if n < nmax. The angles of the flowers in relation to the vertixal apex dimention increase with time; flower stems are modeled using 4th order Bezier splines.

3. Individual Flower Development:
The flowers of this particular plant and many other spring blossoms (cherry, apple) consist of 5 petals, 5 leaflets that are located beneath and in between the petals, and stamena. The flower rewriting can be summarized as follows in terms of these components:

F(P(x1), L(x2), S(x3), AP, AL, width):
&forall i:
    if (x1 &le x1max)
        solve dx/dt = r1 (1 - x1 / x1max) x1;  Pi(x1) &larr P(x1 + &Delta x1)
    if (x2 &le x2max)
        solve dx/dt = r1 (1 - x2 / x2max) x2;  Li(x2) &larr L(x2 + &Delta x2)
    if (x3 &le x3max)
        solve dx/dt = r2 (1 - x3 / x3max) x3;  Si(x3) &larr S(x3 + &Delta x3)
    if (ALi < ALmax) 
        solve dA/dt = r3 (1 - ALi/ALmax) ALi; ALi &larr ALi + &Delta A
    if (APi < APmax) 
        solve dA/dt = r4 (1 - APi/APmax) APi; APi &larr APi + &Delta A
if (width &le widthmax)
    solve dw/dt = r1 (1 - width / widthmax) x3;  width &larr width + &Delta width
where P is a petal, L a leaflet, S a stamen, AP rotation angle of a petal, AL rotation angle of a leaflet, and w is the width of the flower base. The rates for petal, leaflet and bud base growth are nearly idtentical, but are perturbed for every petal and leaflet. The rate of opening (growth rate of angles) for the leaflets is greater than for the petals: r3>r4. A different rate controls the growth and elongation of stamena whose development occurs after the bud has half-opened. The scale of all flower elements is a function of the flower center width.

4. Petals and Leaflets:
These are modeled by 4th order Bezier patches, which in turn are modeled as rewritable skeletons with maximal values for lengths and angles of segments (see diagram for movable limbs labeled Ai and resizable internodes makred Li), approach suggested by [1]. dL-system requires only the start and end skeleton configurations to be specified in order to continuously transform a curved petal into a flat one of an open flower. The petals are texture-mapped with a simple predefined texture that grows lighter linearly with the degree of openness of the bud.

5. Stamena:
There appear to be two types of stamena in the above flowers - the tightly curved purple stamena and white stamena that extend vertically. These are modeled using 4th order Bezier splines, with bases positioned randomly within the center. The splines are modeled by three-armed skeletons: perturbed initial and maximal arm lengths and angles fully determine stamen's development. See diagrams for an example of starting and ending arm configurations (control points in black) and resulting splines.

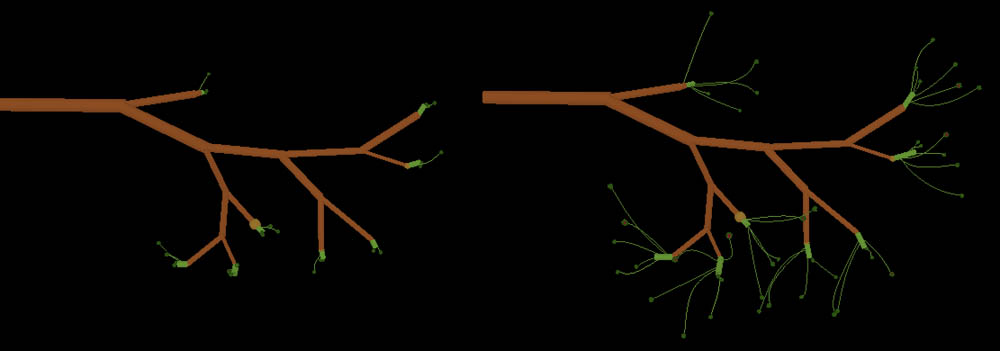
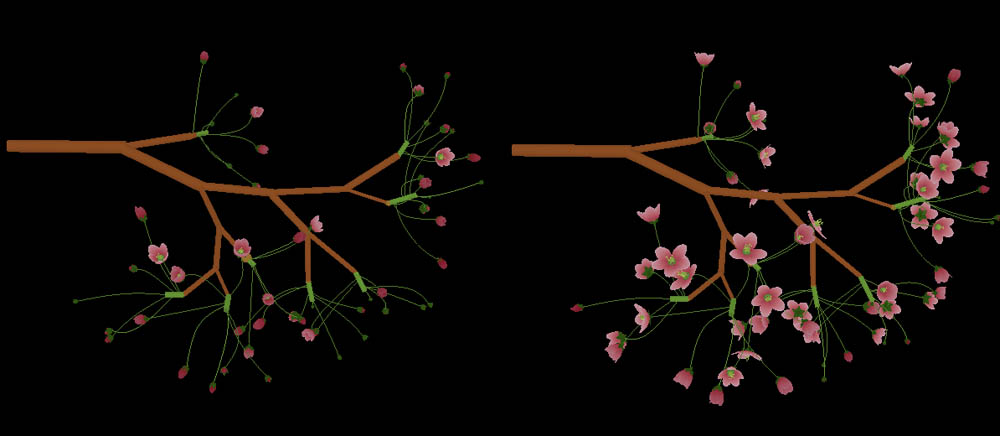
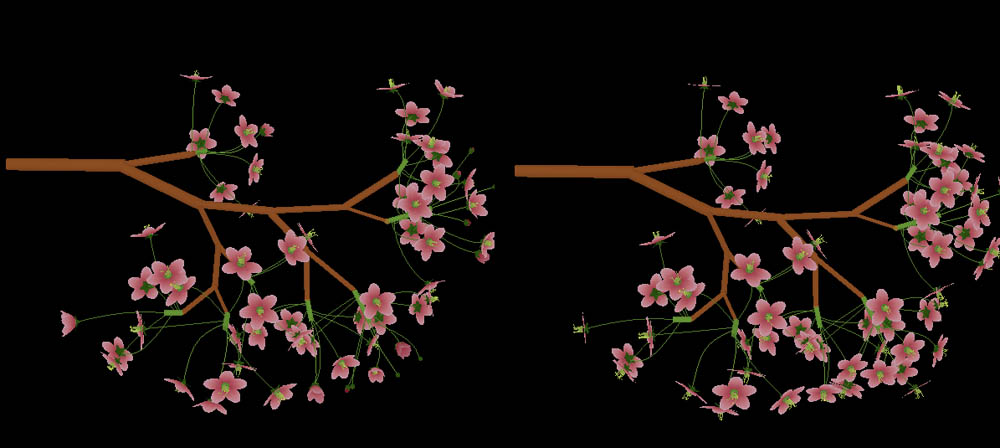
Still Images (click):

References:

1. Prusinkiewicz, Przemyslaw, Mark Hammel and Eric Mjolsness. "Animation of Plant Development." Proceedings of SIGGRAPH '93, pp. 351-360.
2. Prusinkiewicz, Przemyslaw and Aristid Lindenmayer. Algorithmic Beauty of Plants. Springer-Verlag: New York, 1990.

Program:

The program is a simple console application built in VC++. It compiles and runs on Windows using the OpenCV and OpenGL libraries. The most important files in the bundle are modules.cpp and const.h.
Keyboard commands are as follows:
Q: Quit
R: Reset default view
I: Zoom In
O: Zoom Out
G: "Gas" -- speed up animation
B: "Break" -- slow down the animation
S: Start or stop (if already saving) saving video clip into file test01.avi
D: Toggle between views of growing FLOWER, APEX, BRANCH, STAMEN, and PETAL
W: Toggle between Working and non_Working views (mesh v. texture-mapped surfaces)
N: Resets whichever component is displayed to its initial state



Download All Files